ASUPRA UNEI INEGALITĂŢI DATE LA BARAJUL O.B.M.J. 2006

de Mircea Lascu şi Cezar Lupu

La cel de-al cincilea baraj pentru Olimpiada Balcanică de Juniori din data de 20 mai 2006 a fost dată următoarea inegalitate:

Fie x, y, z trei numere reale strict pozitive astfel încât:

.

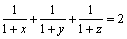Să se arate că .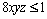

Având în vedere că problema de faţă a fost destul de dificilă pentru elevii prezenţi la testul de selecţie, considerăm că această notă este oportună pentru a ilustra diverse tehnici şi metode în rezolvarea inegalităţilor de acest tip. În acest sens vom da 7 soluţii acestei interesante inegalităţi.

Soluţia 1. Substituţiile 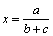, 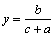şi 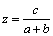verifică egalitatea 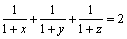, pentru că:

.

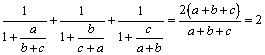Cum aceste numere verifică egalitatea din ipoteză, inegalitatea pe care trebuie s-o demonstrăm se transformă în:

. (*)

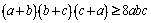Într-adevăr, din inegalitatea mediilor avem:

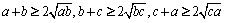
şi prin înmulţirea celor trei inegalităţi rezultă imediat (*).

Soluţia 2. Observăm că egalitatea are loc pentru toate numerele egale cu 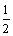. În acest sens, din inegalitatea Cauchy-Buniakovski sau inegalitatea mediilor, avem:

.

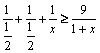Scriind şi analoagele şi adunându-le avem:

. (**)

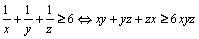Acum vom prelucra egalitatea din ipoteză.

Înmulţind cu 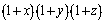, egalitatea este echivalentă cu: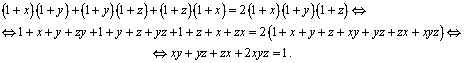

Din (**), utilizând această ultimă egalitate, obţinem concluzia problemei.

Soluţia 3. Este o soluţie directă şi totodată una dintre cele mai uşoare. Am arătat în soluţia precedentă că:

.

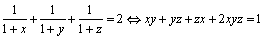Aplicând inegalitatea mediilor în ipoteză obţinem :

.

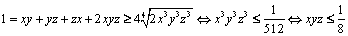Soluţia 4. Prelucrăm ipoteza problemei. Avem:

.

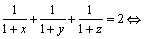
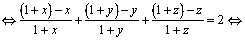
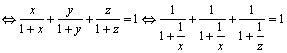Dacă arătăm că 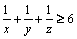, problema este rezolvată.

Notăm 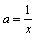, , 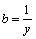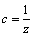. Astfel, trebuie să demonstrăm că:

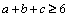dacă .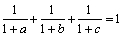

Folosind inegalitatea mediilor sau inegalitatea Cauchy-Buniakovski avem:

,

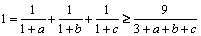de unde avem imediat că .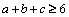

Soluţia 5. Să zicem că nu avem ideea de a face substituţiile din prima soluţie. Pentru aceasta însă vom nota 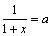, , 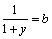, 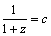de unde:

, , .

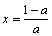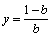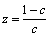Este evident că 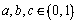. Astfel inegalitatea de demonstrat devine: 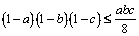cu condiţia 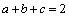. Aplicând inegalitatea mediilor, obţinem:

.

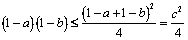Scriind şi analoagele şi înmulţindu-le avem:

.

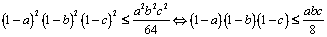Soluţia 6. Egalitatea din ipoteză este echivalentă cu:

.

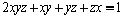Să presupunem prin reducere la absurd că .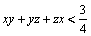

Folosind inegalitatea mediilor vom avea:

.

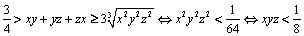Pe de altă parte, folosind ipoteza rezultă .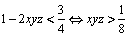

Am obţinut astfel o contradicţie.

Prin urmare, 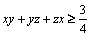şi deci, .

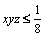Soluţia 7. Să observăm că există 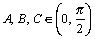astfel încât:

,

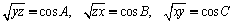pentru că are loc următoarea identitate:

.

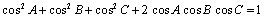Astfel, problema se reduce la a arăta că în orice triunghi ascuţitunghic ABC este adevărată inegalitatea:

.

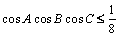Aplicând inegalitatea mediilor şi inegalitatea lui Jensen pentru funcţia concavă cos pe 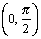, obţinem imediat că:

.

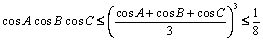În încheiere, pe baza ideilor prezentate, propunem cititorilor să rezolve următoarele probleme:

1. Fie a, b, c trei numere reale strict pozitive care satisfac condiţia:

.

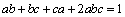Să se arate că: a) 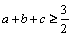; b) .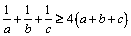

Mircea Lascu şi Marian Tetiva

2. Fie x, y, z trei numere reale pozitive astfel încât:

.

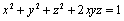Să se arate că:

a) 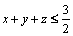; b) ;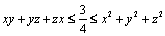

c) .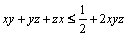

Marian Tetiva

3. Fie x, y, z numere reale pozitive astfel încât 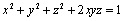. Să se arate că:

.

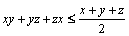Octavian Purcaru, lista scurtă 2003

4. Fie x, y, z numere reale strict pozitive astfel încât:

.

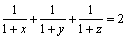Să se arate că:

.

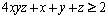5. Fie x, y, z numere reale strict pozitive astfel încât 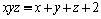. Să se arate că:

a) 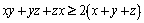; b) .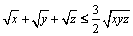

6. Fie a, b, c trei numere reale strict pozitive. Să se arate că:

.

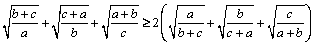Mircea Lascu

7. Fie a, b, c numere reale strict pozitive. Să se arate că:

.

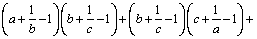
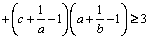Vasile Cârtoaje

8. Fie a, b, c numere reale nenegative astfel încât 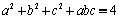. Să se arate că:

.

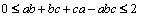Titu Andreescu, USAMO 2001

9. Fie x, y, z numere reale strict pozitive satisfăcând 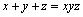. Să se arate că:

.

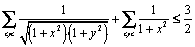Cezar Lupu

10. Fie a, b, c trei numere reale strict pozitive astfel încât 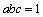. Să se arate că:

.

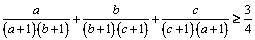Test de Selecţie OIM, Franţa, 2006

11. Fie a, b, c trei numere reale strict pozitive. Să se demonstreze că:

.

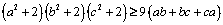Hojoo Lee, APMO 2004

12. Fie x, y, z sunt numere reale pozitive astfel încât 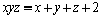. Să se arate că:

.

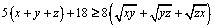Olimpiadă Bosnia-Herţegovina, 2006

Bibliografie

[1] T. Andreescu, V. Cârtoaje, G. Dospinescu, M. Lascu, Old and New Inequalities, Editura GIL, 2004.

Mircea Lascu	Cezar Lupu
Editor,	Student
Editura GIL,	Facultatea de Matematică-Informatică,
Zalău	Universitatea Bucureşti
mail: gil1993@zalau.astral.ro,	mail: lupucezar@yahoo.com