Vom trata câteva probleme de geometrie, care au constituit subiecte de concurs în acest an, dându-le soluţii cât mai simple, cât mai naturale.

1. (Problema 2, olimpiadă, etapa judeţeană, 2006, clasa a VII-a.)

În triunghiul ABC avem . Arătaţi că:

a) ;

b) .

Gh. Bumbăcea, Buşteni

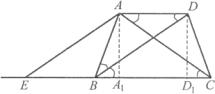Soluţie. a) Fie BE bisectoarea şi D punctul de intersecţie al acesteia cu paralela prin A la latura BC. Conform ipotezei avem că şi în plus (de ce?), deci avem un trapez isoscel în care baza mică este egală cu laturile neparalele.

Aceasta este configuraţia geometrică în care se încadrează „natural“ problema noastră. Fie , şi analog DD₁. Aplicând teorema lui Pitagora în cele două triunghiuri dreptunghice AA₁B şi AA₁C avem că (de ce?).

Dar , deci . Cu alte cuvinte, punctul a) al problemei poate fi „citit“ astfel: „Într-un trapez isoscel în care baza mică este egală cu laturile neparalele, diferenţa dintre pătratul unei diagonale şi pătratul unei laturi neparalele este egală cu produsul bazelor: “.

b) Fie, . În triunghiul EAC avem şi , deci .

2. (Problema 4, olimpiadă, etapa judeţeană, 2006, clasa a VII-a.)

Considerăm ABC un triunghi isoscel cu . Fie D mijlocul laturii BC, M mijlocul segmentului AD şi N piciorul perpendicularei din D pe BM. Arătaţi că .

Marcel Chiriţă, Bucureşti

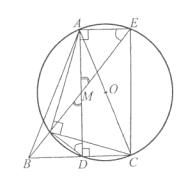Soluţie. Vom utiliza metoda „demonstraţiei inverse“ şi anume vom construi unghiul ANC de măsura 90° cu şi vom arăta că . Dreapta BM intersectează cercul de diametru AC în punctul E. Evident ADCE este dreptunghi (de ce?), iar , deoarece subîntinde diametrul AC.

Deoarece , subîntind acelaşi arc, iar , , rezultă că , adică , deci N este piciorul perpendicularei din D pe BM.

Observaţii. 1. Am preferat prezentarea acestei soluţii tocmai pentru a sugera elevilor configuraţia geometrică simetrică (dreptunghiul ADCE în cercul de diametru AC), în care putem încadra problema.

De altfel, autorul problemei merge pe aceeaşi „cale“, dar evită (poate din motive întemeiate) folosirea cercului.

Exerciţii. Arătaţi că triunghiurile AMN şi CDN sunt asemenea şi determinaţi raportul de asemănare în funcţie de dimensiunile triunghiului iniţial ABC.

3. (Problema 3, olimpiadă, etapa naţională, 2006, clasa a VII-a.)

Triunghiul ascuţitunghic ABC are unghiul C cu măsura de 45°. Punctele A₁ şi B₁ sunt picioarele înălţimilor din A şi B, iar H este ortocentrul triunghiului. Considerăm punctele D şi E situate pe segmentele AA₁ şi BC cu proprietatea că . Demonstraţi că:

a) ; .

Claudiu-Ştefan Popa, Iaşi

Soluţie. a) Vom considera configuraţia geometrică în care apare cercul de diametru CH. Vom nota acest cerc cu şi vom vedea cum acesta lămureşte semnificaţiile relaţiilor din enunţ. Deoarece , rezultă că , unghiul la centru corespunzător unghiului ; deoarece rezultă că:

, (1).

În plus, (de ce?), deci . În triunghiul dreptunghic HA₁C avem că:

, (2).

Din (1) şi (2) rezultă că , adică

.

b) Conform ipotezei avem că , deci .

Observaţii. 1) Deoarece reprezintă media pătratică a lungimilor A₁B şi A₁C, avem că:

,

unde M este mijlocul laturii BC şi, evident (de ce?); am dat astfel o interpretare geometrică a inegalităţii dintre media pătratică şi media aritmetică.

2) Problema este valabilă şi în cazul când triunghiul este obtuzunghic.

Reluaţi demonstraţia punctelor a) şi b) în acest caz.

4. (Problema 1, olimpiadă, etapa naţională, 2006, clasa a VII-a.)

Considerăm ABC un triunghi şi punctele M şi N aparţin laturilor AB, respectiv BC astfel încât . Fie P un punct pe dreapta AC. Să se arate că dreptele MN şi NP sunt perpendiculare dacă şi numai dacă PN este bisectoarea unghiului MPC.

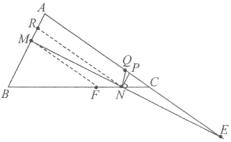Soluţie. Dacă plecăm de la concluzia problemei echivalenţa pe care trebuie să o verificăm este totuna cu următoarea problemă: dat punctul M pe latura AB, trebuie să construim o dreaptă MN, astfel încât ea intersectează dreapta AC în punctul E cu proprietatea .

Construcţia este următoarea: considerăm mijlocul R al segmentului AM şi ducem prin R o paralelă la AC, care taie BC, respectiv AC în N, respectiv E.

Evident, în triunghiul AME, RN este linie mijlocie faţă de latura AE, deci . În această situaţie este mediatoarea segmentului .

Rămâne de verificat condiţia (de ce?).

Observaţii. 1) Am ales această prezentare a soluţiei pentru a pune în evidenţă construcţia efectuată de autor în demonstraţia dată.

2) La aceeaşi configuraţie geometrică ajungeam dacă duceam prin M o paralelă la AC, care intersecta BC în F şi apoi înjumătăţeam segmentul FC prin punctul N (de ce?).

5. (Problema 2, olimpiadă, etapa naţională, 2006, clasa a IX-a.) Se consideră triunghiurile isoscele ABC şi DBC având baza BC şi . Fie M mijlocul segmentului BC. Punctele E, F, P sunt alese astfel încât , , , iar . Să se arate că P este mijlocul segmentului EF şi .

Manuela Prajea, Drobeta Tr. Severin

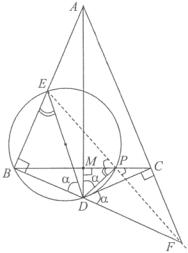Soluţie. Vom apela din nou la „demonstraţia inversă“. Construim unghiul BDE, , de măsură şi cercul de diametru DE care intersectează segmentul (MC) în punctul P. Din construcţie avem că ; , subîntind acelaşi arc; dar , deci şi complementarele lor vor fi egale: , deci punctul P este cel „ales“ în ipoteza problemei.

Prelungim dreapta EP până intersectează AC în punctul F, deci . În plus, . Deci patrulaterul DPCF este inscriptibil, în cercul de diametru DF. Rezultă că , deci punctul F este cel „ales“ în ipoteza problemei.

În concluzie, punctele E, P, F sunt alese ca în ipoteză, ele sunt coliniare (din construcţie) şi (tot din construcţie).

Rămâne de arătat că , ceea ce este totuna cu a arăta că DP este bisectoarea unghiului (de ce?). Pentru aceasta este suficient să observăm că (de ce?).

Observaţii. 1) Soluţia autoarei problemei este cea naturală; ea sugerează folosirea transformărilor geometrice (a rotaţiei de vârf D şi unghi şi a omotetiei de acelaşi vârf). Aceste tehnici sunt indispensabile în logistica oricărui „finalist“; pe cât de indispensabile, pe atât de neglijate în favoarea tehnicilor de calcul algebric (vectorial).

2) Am preferat soluţia de mai sus pentru a reconfirma utilitatea „demonstraţiei inverse“, în unele situaţii; în plus, „am manevrat“ cu unghiurile şi figurile inscriptibile, ceea ce este şi la îndemâna unui elev bun de gimnaziu.

3) Se putea observa „dintru bun început“, că în condiţiile ipotezei avem congruenţa triunghiurilor DBE şi , deci . Mai rămâne de arătat că cercurile congruente de diametre DE şi DF se mai intersectează o dată într-un punct P care se află pe dreapta BC (DP fiind axa radicală a celor două cercuri). Continuaţi demonstraţia pe această cale.

Profesor,

C.N. „Spiru Haret“, Bucureşti