Articole interesante din Gazeta Matematică
Dacă astazi România înregistrează perfomanţă în matematică este pentru că şcoala de matematică românească se sprijină pe umerii acestor uriaşi.
Vă prezentăm în această secţiune cele mai interesante articole matematice care au făcut istorie de-a lungul timpului în Gazeta Matematică.
Dacă aţi descoperit articole şi credeţi că sunt de un interes mai larg, vă invităm să ne semnalaţi acest lucru trimiţându-ne numele articolelor, numărul Gazetei, anul în care au aparut. Administratorul siteului va hotarî dacă acestea vor fi publicate.
Gheorghe Ţiţeica - Gazeta Matematică, nr. 3 din 1908
Rezolvarea în
numere întregi a ecuaţii ![]()
Problema aceasta
e veche şi rezolvată de mult. Soluţiuni parţiale, ca ![]() ,
, ![]() ,
, ![]() , sau
, sau ![]() ,
, ![]() ,
, ![]() , erau cunoscute şi întrebuinţate în practică
de popoarele din antichitate odată cu primele începuturi de
civilizaţie. (Vezi articolul Ultima teoremă a lui Fermat al
D-lui. I. Ionescu, în Natura, Octomvrie 1908).
, erau cunoscute şi întrebuinţate în practică
de popoarele din antichitate odată cu primele începuturi de
civilizaţie. (Vezi articolul Ultima teoremă a lui Fermat al
D-lui. I. Ionescu, în Natura, Octomvrie 1908).
In articolul de faţă vreau să dau o metodă geometrică de a găsì toate soluţiunile, care e aşà de simplă şi intuitivă, încât fără să ştiu, poate, să fi fost cu toate acestea dată de cineva. Chiar dacă ar fi aşà nu e nici o pagubă pentru cititorii Gazetei.
1. Iată
în ce consistă metoada. Să lăsăm la o parte soluţia ![]() ,
, ![]() ,
, ![]() ; atunci Z e diferit de zero şi putem
împărţi toţi termeni cu Z2. Atunci punând :
; atunci Z e diferit de zero şi putem
împărţi toţi termeni cu Z2. Atunci punând :
(1) ![]() ,
, ![]()
obţinem ecuaţia :
(2) ![]() ,
,
care, în raport cu două axe perpendiculare, reprezintă un cerc. La trei numere întregi care verifică ecuaţia dată corespunde, cu ajutorul formulelor (1), un punct al cercului (2) cu coordonate raţionale — adică fracţionare — sau cum vom zice mai scurt, un punct raţional. Invers, unui punct raţional de pe cercul (2) îi corespunde — precum vom vedeà de altfel mai de aproape la sfârşitul acestui articol — o soluţie în numere întregi a ecuaţii date.
Am redus prin urmare problema dată la căutarea punctelor raţionale aşezate pe cercul (2).
Găsirea
tutulor acestor puncte se întemeiază pe observarea că e destul
să cunoaştem un punct raţional ![]() al cercului, pentru
ca să le putem aflà apoi pe toate. Intr’adevăr, orice alt punct
raţional
al cercului, pentru
ca să le putem aflà apoi pe toate. Intr’adevăr, orice alt punct
raţional ![]() al cercului unit cu M0 ne dă o dreaptă a cărei ecuaţie :
al cercului unit cu M0 ne dă o dreaptă a cărei ecuaţie :
![]()
are coeficienţii raţionali, sau mai pe scurt, dreapta M1M0 e o dreaptă raţională. Prin urmare punctele raţionale ale cercului nu se pot găsì decât printre punctele de intersecţie ale cercului cu dreptele raţionale cari trec prin M0. Vreau însă să arăt că toate aceste puncte de intersecţie sunt raţionale.
Pentru aceasta, fie
(3) ![]()
o dreaptă
raţională arbitrară care trece prin M0, în care deci m este număr raţional. Eliminând pe y între (3) şi (2)
căpătăm o ecuaţie de gradul al doilea cu coeficienţi
raţionali şi care are ca rădăcini abscisele punctelor de
intersecţie ale dreptei (3) cu cercul (2), prin urmare
neapărat pe x0 şi încă altă valoare ![]() tot
raţională. Abscisa
tot
raţională. Abscisa ![]() a punctului al doilea
de intersecţie fiind raţională, rezultă din (3) că
şi ordonata sa e raţională şi atunci punctul acela e
raţional. Aşà dar, orice dreaptă raţională dusă
prin punctul raţional cunoscut M0 ne mai determină un
punct raţional al cercului şi, după cum arătarăm,
aşà se obţin toate.
a punctului al doilea
de intersecţie fiind raţională, rezultă din (3) că
şi ordonata sa e raţională şi atunci punctul acela e
raţional. Aşà dar, orice dreaptă raţională dusă
prin punctul raţional cunoscut M0 ne mai determină un
punct raţional al cercului şi, după cum arătarăm,
aşà se obţin toate.
Insă pe
cercul (2) avem punctul raţional ![]() . Cu ajutorul lui putem să aflăm prin urmare toate
punctele raţionale ale cercului. Dar înnainte de a da formulele explicite,
să mai facem o observare. Din cauza simetrii, ne putem mulţumì
să aflăm punctele raţionale din unghiul pozitiv al axelor,
adică pentru care
. Cu ajutorul lui putem să aflăm prin urmare toate
punctele raţionale ale cercului. Dar înnainte de a da formulele explicite,
să mai facem o observare. Din cauza simetrii, ne putem mulţumì
să aflăm punctele raţionale din unghiul pozitiv al axelor,
adică pentru care ![]()
![]() . Atunci, dacă însemnăm cu B punctul de coordonate
. Atunci, dacă însemnăm cu B punctul de coordonate ![]() ,
, ![]() şi cu AT
tangenta în A la cerc, dreapta raţională arbitrară pe care o
ducem prin punctul A trebue să fie cuprinsă în unghiul ascuţit
BAT şi prin urmare coeficientul unghiular m din
ecuaţia (3) trebue să fie un număr raţional cuprins
între
şi cu AT
tangenta în A la cerc, dreapta raţională arbitrară pe care o
ducem prin punctul A trebue să fie cuprinsă în unghiul ascuţit
BAT şi prin urmare coeficientul unghiular m din
ecuaţia (3) trebue să fie un număr raţional cuprins
între ![]() şi
şi ![]() . Putem pune în (3) :
. Putem pune în (3) :
![]() ,
, ![]() ,
, ![]()
în care numerele
întregi p şi q sunt pozitive, prime între ele şi ![]() şi avem :
şi avem :
![]()
![]()
Introducând
această valoare a lui y în (2) şi suprimând soluţia ![]() , care ne dă din nou punctul A, găsim :
, care ne dă din nou punctul A, găsim :
![]() ,
,
şi din ![]() deducem :
deducem :
![]() .
.
Avem prin urmare rezultatul următor : Toate numerele raţionale şi pozitive cari verifică ecuaţia (2) sunt date de formulele :
![]() ,
, ![]() ,
,
în care p, q
sunt numere întregi şi pozitive, prime între ele şi ![]() .
.
2. Acum, după ce am rezolvat problema ajutătoare, să ne întoarcem la problema noastră. Şi mai întâi o observare. E evident că dacă X, Y, Z sunt soluţii ale problemei, şi kX, kY, kZ vor fi soluţii, k fiind un număr întreg arbitrar. E natural prin urmare să ne ocupăm numai de acele soluţii în care X, Y, Z sunt prime între ele, adică nu au nici un divizor comun. Acele soluţii verifică, din cele ce preced, următoarele egalităţi :
![]() ,
, ![]()
sau :
(4) ![]()
în care p şi q satisfac condiţiunilor enunţate mai înnainte. De
oarece X, Y, Z trebuesc să fie numere întregi şi pentrucă p şi q sunt numere întregi, rezultă că în (4) valoarea
comună k a celor trei rapoarte egale este un număr
raţional. Se poate pune evident ![]() , a şi b fiind două numere întregi
prime între ele şi atunci din (4) scoatem :
, a şi b fiind două numere întregi
prime între ele şi atunci din (4) scoatem :
![]() ,
, ![]() ,
, ![]()
şi b va trebuì ales aşà ca X, Y, Z să fie numere întregi prime între ele.
Insă b e prim cu a, deci trebueşte să dividă
pe ![]() , 2pq şi
, 2pq şi ![]() . Rezultă atunci că a este un divizor comun
numerelor întregi X, Y, Z şi, potrivit unei observări făcute, îl
putem lăsà la o parte. Aşà dar avem :
. Rezultă atunci că a este un divizor comun
numerelor întregi X, Y, Z şi, potrivit unei observări făcute, îl
putem lăsà la o parte. Aşà dar avem :
![]() ,
, ![]() ,
, ![]() .
.
Numărul
întreg b este sau 1 sau, de se poate, un divizor comun al numerelor ![]() , 2pq,
, 2pq, ![]() . Acest divizor comun este un divizor comun şi numerelor
. Acest divizor comun este un divizor comun şi numerelor ![]() ,
, ![]() , deci nu poate fi, dacă este, decât 2, căci p şi q fiind prime între ele şi p2 şi q2 vor fi prime între ele. Aşa dar avem
, deci nu poate fi, dacă este, decât 2, căci p şi q fiind prime între ele şi p2 şi q2 vor fi prime între ele. Aşa dar avem ![]() sau
sau ![]() .
.
Când vom aveà ![]() şi când
şi când ![]() ? Vom aveà
? Vom aveà ![]() , dacă
, dacă ![]() şi
şi ![]() sunt numere cu
soţ, căci 2pq se divide evident cu 2. Vom aveà
sunt numere cu
soţ, căci 2pq se divide evident cu 2. Vom aveà ![]() , când unul din numerele
, când unul din numerele ![]() şi
şi ![]() va fi fără
soţ. Insă, în privinţa numerelor p şi q putem
face numai două ipoteze : sau sunt amândouă fără
soţ, sau numai unul e fără soţ. Amândouă cu soţ
nu pot fi, căci ar urmà să nu fie prime între ele. In primul caz,
când p şi q sunt fără soţ, atunci
va fi fără
soţ. Insă, în privinţa numerelor p şi q putem
face numai două ipoteze : sau sunt amândouă fără
soţ, sau numai unul e fără soţ. Amândouă cu soţ
nu pot fi, căci ar urmà să nu fie prime între ele. In primul caz,
când p şi q sunt fără soţ, atunci ![]() şi
şi ![]() sunt cu soţ
şi deci luăm :
sunt cu soţ
şi deci luăm :
![]() ,
, ![]() ,
, ![]()
şi se vede că X, Y, Z sunt întregi şi prime între ele.
In al doilea caz,
când p şi q nu sunt amândouă fără soţ, ![]() şi
şi ![]() sunt fără
soţ şi atunci luăm :
sunt fără
soţ şi atunci luăm :
![]() ,
, ![]() ,
, ![]() .
.
Astfel am găsit toate soluţiunile în numere întregi ale ecuaţii :
![]() .
.
G. Ţiţeica.
Traian Lalescu - Gazeta Matematică, nr. 11 din 1910
Asupra Pendulului lui Foucault
(Comunicare făcută la Soc. de Ştiinţe, Şedinţa de la 7 Iunie 1911)
1. In studiul mişcării pendulului lui Foucault, adică al mişcării unui pendul sferic, ţinând seama de mişcarea de rotaţie diurnă a pământului, se obţin ecuaţiunile generale bine cunoscute :

Aceste ecuaţii sunt dificile de integrat ; ele se înlocuesc prin ecuaţiile aproximative :

obţinute din primele în ipotesa ![]() . Ecuaţia treia ne dă în acest cas, cu multă aproximaţie, în mod direct
. Ecuaţia treia ne dă în acest cas, cu multă aproximaţie, în mod direct ![]() .
.
Ecuaţiile (2) sunt supuse de obicei – în tratatele pe cari le cunosc eu cel puţin – unui calcul fastidios care are desavantajul că este şi aproximativ.
Imi propun să indic acì o metodă exactă care ne permite să terminăm, pe o cale mult mai lesnicioasă, această chestiune.
2. Dacă în ecuaţiile (2) ar lipsì termenii ![]() şi
şi ![]() , ele ar reprezentà mişcarea bine cunoscută a unui punct atras de o forţă proporţională cu distanţa ; traectoria ar fi în acest cas o elipsă având centrul în origină. Să considerăm o asemenea mişcare pe o elipsă al cărei parametru de atracţie să fie în mod general k2, şi să imprimăm elipsei o mişcare de rotaţie uniformă de vitesă unghiulară
, ele ar reprezentà mişcarea bine cunoscută a unui punct atras de o forţă proporţională cu distanţa ; traectoria ar fi în acest cas o elipsă având centrul în origină. Să considerăm o asemenea mişcare pe o elipsă al cărei parametru de atracţie să fie în mod general k2, şi să imprimăm elipsei o mişcare de rotaţie uniformă de vitesă unghiulară ![]() şi în sens retrograd. In acest cas avem o compunere de mişcări, aşà că acceleraţia mişcării ne este dată de formula lui Coriolis :
şi în sens retrograd. In acest cas avem o compunere de mişcări, aşà că acceleraţia mişcării ne este dată de formula lui Coriolis :
![]() .
.
Insă acceleraţia relativă gr are drept compunătoare : ![]() ,
, ![]() , 0 ; acceleraţia de târâre :
, 0 ; acceleraţia de târâre : ![]() ,
, ![]() , 0 ; în sfârşit de oarece avem :
, 0 ; în sfârşit de oarece avem : ![]() ,
, ![]() , compunătoarele acceleraţiei lui Coriolis vor fi :
, compunătoarele acceleraţiei lui Coriolis vor fi : ![]() ,
, ![]() .
.
Ecuaţiunile mişcării punctului de pe elipsă vor fi atunci :
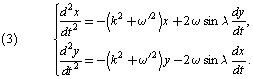
Ecuaţiunile (3) sunt absolut de aceaşi formă ca ecuaţiunile (2) şi devin identice cu acestea dacă punem :
![]() .
.
Prin urmare, mişcarea punctului ![]() se va face pe o elipsă, al cărei parametru de atracţie este perturbat de cantitatea
se va face pe o elipsă, al cărei parametru de atracţie este perturbat de cantitatea ![]() ; la rândul său această elipsă e animată de o mişcare de rotaţie uniformă în jurul centrului său, în sens retrograd şi cu vitesa unghiulară
; la rândul său această elipsă e animată de o mişcare de rotaţie uniformă în jurul centrului său, în sens retrograd şi cu vitesa unghiulară ![]() .
.
Succesul acestei metode provine din faptul că acceleraţia de târâre are exact aceeaşi formă ca şi acceleraţia relativă.
După cum se vede, metoda precedentă ne arată că aproximaţia care se face de obicei în al doilea rând în această chestiune, aproximaţie care, după cum se vede nu este indispensabilă, nu atinge perioada mişcărei de rotaţie a elipsei, ci numai pe aceea a punctului depe elipsă.
Tr. Lalescu.
Dan Barbilian - Gazeta Matematică, nr. 11 din 1928
*LINIILE FRÂNTE ECHILATERE, INSCRISE UNUI ACELAŞ UNGHIU
Fie axele ![]() şi
şi ![]() care se
intersectează în O. Să considerăm vectorul
care se
intersectează în O. Să considerăm vectorul ![]() , cu origina pe axa
, cu origina pe axa ![]() şi extremitatea
pe
şi extremitatea
pe ![]() . Se poate constatà uşor că orice alt vector
. Se poate constatà uşor că orice alt vector ![]() , echipolentic cu
, echipolentic cu ![]() şi având origina
şi extremitatea pe aceleaşi axe, se confundă neapărat cu
acesta.
şi având origina
şi extremitatea pe aceleaşi axe, se confundă neapărat cu
acesta.
Intr’adevăr,
lăsând la o parte condiţia ca extremitatea B1 să se
găsească pe axa ![]() , locul ei geometric e o paralelă (unică) la
, locul ei geometric e o paralelă (unică) la ![]() , care taie pe
, care taie pe ![]() în A1.
Deci, problema înscrierii într’un anumit unghiu, a unui segment echipolentic cu
un segment dat, are o singură soluţie, ceeace justifică
afirmarea făcută mai sus.
în A1.
Deci, problema înscrierii într’un anumit unghiu, a unui segment echipolentic cu
un segment dat, are o singură soluţie, ceeace justifică
afirmarea făcută mai sus.
Aşà fiind,
cu plecare dela segmentul A0A1, să construim o linie
frântă A0A1A2A3A4A5....A2n,
cu vârfurile pare pe axa ![]() şi cele impare,
pe axa
şi cele impare,
pe axa ![]() , aşà încât :
, aşà încât :
![]()
Această construcţie se poate executà foarte uşor, cu compasul.
Să
observăm că trecerea dela vectorul ![]() la vectorul
la vectorul ![]() se face printr’o
simetrie faţă de o axă perpendiculară pe
se face printr’o
simetrie faţă de o axă perpendiculară pe ![]() . Trecerea dela vectorul
. Trecerea dela vectorul ![]() , la
, la ![]() se face printr’o
simetrie faţă de o altă axă, perpendiculară pe
se face printr’o
simetrie faţă de o altă axă, perpendiculară pe ![]() . Compunerea a două simetrii dă naştere la
o rotaţie, de unghiu de două ori mai mare ca unghiul axelor de
simetrie.
. Compunerea a două simetrii dă naştere la
o rotaţie, de unghiu de două ori mai mare ca unghiul axelor de
simetrie.
Fie ![]() unghiul pozitiv pe
care axa
unghiul pozitiv pe
care axa ![]() îl face cu
îl face cu ![]() . Axele de simetrie, perpendiculare pe acestea, vor face
între ele un unghi egal tot cu
. Axele de simetrie, perpendiculare pe acestea, vor face
între ele un unghi egal tot cu ![]() .
.
Conchidem deci
că vectorul ![]() se duce din
se duce din ![]() printr’o rotire de
amplitudine
printr’o rotire de
amplitudine ![]() (centrul de rotaţie nu ne
interesează).
(centrul de rotaţie nu ne
interesează).
La fel se
dovedeşte că ![]() se deduce din
se deduce din ![]() printr’o rotire de
unghi
printr’o rotire de
unghi ![]() ; sau, direct, din
; sau, direct, din ![]() , după o rotire de unghi
, după o rotire de unghi ![]() . Vectorul
. Vectorul ![]() se deduce din
se deduce din ![]() după o rotire de
unghi
după o rotire de
unghi ![]() , etc.....
, etc.....
In general,
vectorul ![]() , se deduce din vectorul iniţial
, se deduce din vectorul iniţial ![]() după o rotire de
unghi
după o rotire de
unghi ![]() .
.
O condiţie
necesară (fără a puteà spune deocamdată că e şi
suficientă) ca linia noastră poligonală să se închidă
după operaţia de rang 2n, e ca ultimul vector ![]() să devină
echipolent cu primul,
să devină
echipolent cu primul, ![]() , adică amplitudinea
, adică amplitudinea ![]() să se
reducă la un multiplu de
să se
reducă la un multiplu de ![]() . După cum vedem această condiţie se
referă numai la unghiul celor două axe
. După cum vedem această condiţie se
referă numai la unghiul celor două axe ![]() şi
şi ![]() ; nicidecum la segmentul A0A1, dela care am început să înscriem linia poligonală.
; nicidecum la segmentul A0A1, dela care am început să înscriem linia poligonală.
Cevà mai
mult : pentruca operaţia de rangul 2n să fie cea
dintâi care aduce vectorul ![]() echipolent cu
echipolent cu ![]() , trebuie şi este deajuns ca
, trebuie şi este deajuns ca ![]() să fie o
fracţiune ireductibilă, de numitor 2n dintr’o
semicircumferinţă, adică
să fie o
fracţiune ireductibilă, de numitor 2n dintr’o
semicircumferinţă, adică
1) ![]()
unde m şi n sunt prime între ele.
Dar această
condiţie, necesară pentru închiderea construcţiei este
şi suficientă, în virtutea observaţiei făcute la
început, anume că doi vectori ![]() şi
şi ![]() echipolenţi
şi înscrişi în acelaş unghi, se confundă.
echipolenţi
şi înscrişi în acelaş unghi, se confundă.
Avem prin urmare următoarea propoziţie :
Unghiurile egale cu o fracţiune ireductibilă, de numitor n, dintr’un semicerc, sunt singurele capabile de un poligon echilater de 2n laturi înscris în unghi. Una din laturile poligonului poate fi aleasă după voie, toate celelalte se deduc succesiv printr’o construcţie uşoară, cu ajutorul compasului.
*
* *
Exemplul cel mai simplu de unghi capabil de un poligon echilater este, evident, acela care corespunde cazului
![]() ,
,
adică unghiului drept. E clar că într’un astfel de unghi se pot înscrie o infinitate de romburi de latură arbitrară.
Imediat următor e cazul unghiului de 60° :
![]() .
.
Problema înscrierii unui exagon echilater de latură arbitrară, într’un unghi de 60° a fost propusă anul acesta la concursul G. M. (teza de Geometrie, cl. IV). Demonstraţia se poate face, pentru acest caz, pe cale cu totul elementară.
Pentru a precizà, să presupunem că în triunghiul A0OA1, unghiul din A0 e mai mic ca unghiul din A1 ; se vede numai decât că avem atunci :
![]()
![]() .
.
După o teoremă cunoscută (la unghiul mai mare se opune latura mai mare) avem :
![]() .
.
Această neegalitate arată că oblica A2O e mai scurtă decât oblicele egale A1A0 şi A1A2 ; deci punctul O vine între A1 şi A2. Din aproape în aproape, prin raţionamente echivalente, se demonstrează că punctul O este interior segmentului A1A3 ; exterior, lui A2A4 ; iarăşi interior, lui A3A5 ; interior de asemenea lui A4A6.
Fie acum A1P
perpendiculara din A1 pe ![]() şi
şi ![]() oblica egală cu
A1O. Se vede numai decât că triunghiul
oblica egală cu
A1O. Se vede numai decât că triunghiul ![]() e echilateral. Pe de
altă parte triunghiurile OA1A2 şi
e echilateral. Pe de
altă parte triunghiurile OA1A2 şi ![]() sunt simetrice
faţă de A1P, deci egale. Prin urmare
sunt simetrice
faţă de A1P, deci egale. Prin urmare
![]() .
.
Avem egalitatea următoare, urmată de alte patru egalităţi, deduse pe aceeaşi cale :
![]()
![]()
![]()
![]()
![]() .
.
Comparând aceste egalităţi scoatem imediat
![]() .
.
Dar s’a observat că A0 şi A6 vin pe aceeaşi axă şi de aceeaşi parte faţă de O ; aşà dar coincid.
Q. E. D.
*
* *
Această problemă, în cazul ei general, am propus-o la Cercul de Geometrie Elementară al studenţilor în matematici, anul I. Domnul G. Theiler a dat problemei o soluţie ingenioasă, însă necomplectă.
Domnul Profesor Ţiţeica mi-a atras
atenţia că problema subsistă şi în cazul a două axe ![]() şi
şi ![]() arbitrare, în
spaţiu.
arbitrare, în
spaţiu.
Această proprietate a unghiului a cărui valoare e o fracţiune raţională dintr’o semicircumferinţă am găsit-o întâi pe o altă cale, care poate prezentà interes întrucât leagă această chestiune elementară de teoreme de închidere mai complicate.
Fie segmentul A0A1 de lungime dată l, care se sprijină în mişcarea lui pe
axele ![]() şi
şi ![]() de unghi
de unghi ![]() . Insemnând cu x şi y abscisele
. Insemnând cu x şi y abscisele ![]() şi
şi ![]() , avem legătura :
, avem legătura :
2) ![]() .
.
Diferenţiând, obţinem :
3) ![]() .
.
Dar avem, identic, în virtutea lui 2) :
![]() ;
; ![]() .
.
Astfel ecuaţia diferenţială 3) se reduce la o ecuaţie Euler, degenerată :
4) ![]()
care se integrează numai decât, exprimând pe x şi y prin funcţiuni uniforme de două argumente u şi v :
5) ![]() ,
, ![]() .
.
Avem, în virtutea acestei substituţii
![]() ,
,
a cărei integrală generală este evident
6) ![]()
unde C e o constantă. Pentru determinarea ei să luăm cosinusul :
![]()
sau, înlocuind cu valorile 5) :
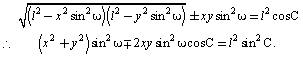
Pentru ca
această ecuaţie să se identifice cu 2) putem luà ![]() , cu condiţia ca să alegem pentru formulă
semnul superior (minus).
, cu condiţia ca să alegem pentru formulă
semnul superior (minus).
Avem astfel, conform lui 6) :
![]() ,
,
Să
însemnăm cu u2i argumentele corespunzătoare
punctelor A2i şi cu ![]() argumentele
corespunzătoare punctelor
argumentele
corespunzătoare punctelor ![]() .
.
Avem, conform lui 7) :
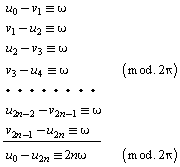
Condiţia necesară şi suficientă pentru închidere este deci
![]() .
.
D. Barbilian.